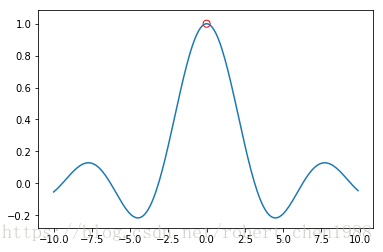
# inf&min与sup&max 在看论文时，发现有些论文写inf，而不是min，遂生疑惑。  查了查发现定义如下： inf 是 infimum 的简称，指一个集合最小的上界(上确界)。 sup 是 supremum 的简称，指一个集合最大的下界(下确界)。 使用 inf 或 sup 总能保证一个函数的 inf 或 sup 存在，而函数的 min 或 max 有时候不存在。 这篇[博客](https://blog.csdn.net/robert_chen1988/article/details/81233738)中举了个例子： f ( x ) = sin ⁡ ( x ) / x 的图像如下：  该函数在 x = 0 处没有值，因此其最大值即 max 不存在，但是我们可以看出 f(x) 最小的上界为 1（不小于它最大值的值，都是它的上界），即 sup ⁡ f ( x ) = 1。